When you already know the algorithm you want to implement, why should you use test-driven development to write it? And how do you test-drive a known algorithm or formula?
Intro (TL;DR)
I needed a function that, given a percentage value, returns an x and y coordinate on a circle so that a pie slice drawn with this end coordinate represents that percentage.
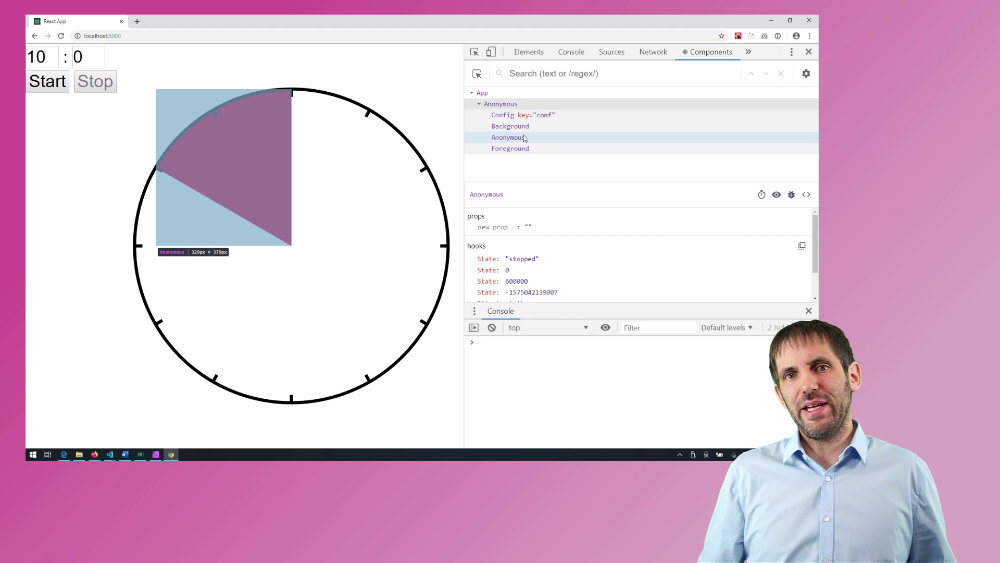
I needed this function because I wrote a simple timer application in a test-driven way, using React. I did this because I teach React trainings and also TDD trainings, and I needed some new examples. The timer shows the remaining time as a pie slice, and it uses a few React components to render the graphics and the configuration panel.
Question / Problem
So, getting x and y coordinates on a circle, given the percentage of a circle… That should only be two calls to the built-in sinus and cosinus functions. Why should I want to write this function - a function that could be a one-liner - in a test-driven way?
In this case, the resulting formula is simple, but I was sure that I would get something wrong at the first try. Is it sinus or minus sinus? Is x the sinus and y the cosinus or vice versa?
Even though I basically knew the formula, I wanted to write a few tests to pin the edge cases down.
But which tests should I write? How many tests do I need to help me implement the code? Which tests could I need later to catch regressions?
Solution
In this case, I decided to test only three points on the circle. Because I already knew the formula, I only wanted to make sure that I did not accidentally switch cosinus and sinus and that I get the signs of both right.
Also, I hope that noone will change this implementation to something completely incompatible, like not using cosinus and sinus at all. So, three points that check for signs and order will also hopefully be enough to catch regressions later.
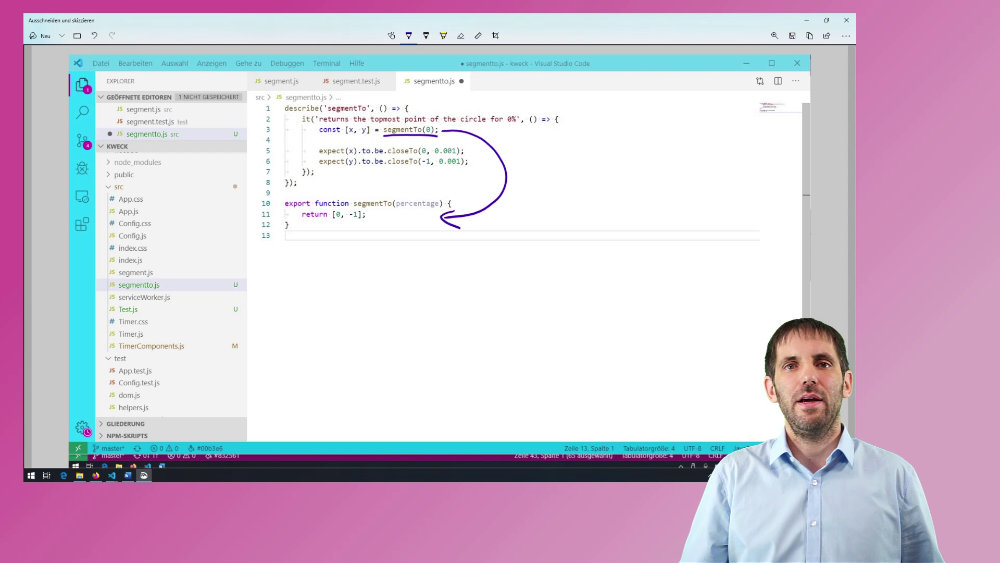
I started with testing the topmost point, but for now, this test would only define the API of the production code.
describe('segmentTo', () => {
it('returns the topmost point of the circle for 0%', () => {
const [x, y] = segmentTo(0);
expect(x).to.be.closeTo(0, 0.001);
expect(y).to.be.closeTo(-1, 0.001);
});
});
export function segmentTo(percentage) {
return [0, -1];
}
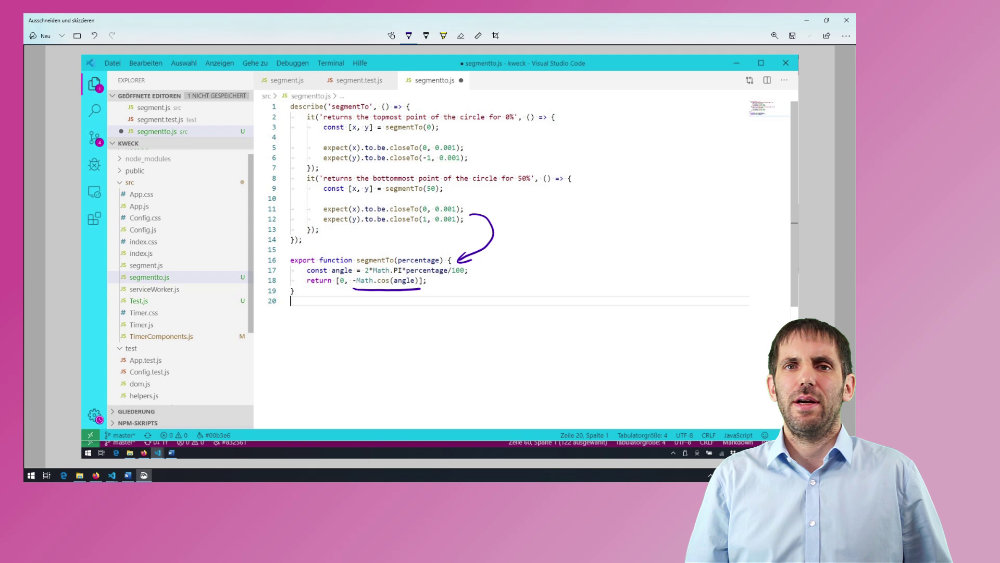
I used the next test to pin down the code for the y coordinate. Because I knew that the final result would be a combination of sinus and cosinus and by looking at the fake implementation of segmentTo after the first test, I decided to use minus cosinus for the y coordinate.
describe('segmentTo', () => {
//...
it('returns the bottommost point of the circle for 50%', () => {
const [x, y] = segmentTo(50);
expect(x).to.be.closeTo(0, 0.001);
expect(y).to.be.closeTo(1, 0.001);
});
});
export function segmentTo(percentage) {
const angle = 2*Math.PI*percentage/100;
return [0, -Math.cos(angle)];
}
I now only needed one more test to finish the implementation. I already know that the other coordinate should either be sinus or minus sinus. By writing the last test, I then was sure that it would be minus sinus.
describe('segmentTo', () => {
//...
it('returns the leftmmost point of the circle for 25%', () => {
const [x, y] = segmentTo(25);
expect(x).to.be.closeTo(-1, 0.001);
expect(y).to.be.closeTo(0, 0.001);
});
});
export function segmentTo(percentage) {
const angle = 2*Math.PI*percentage/100;
return [-Math.sin(angle), -Math.cos(angle)];
}
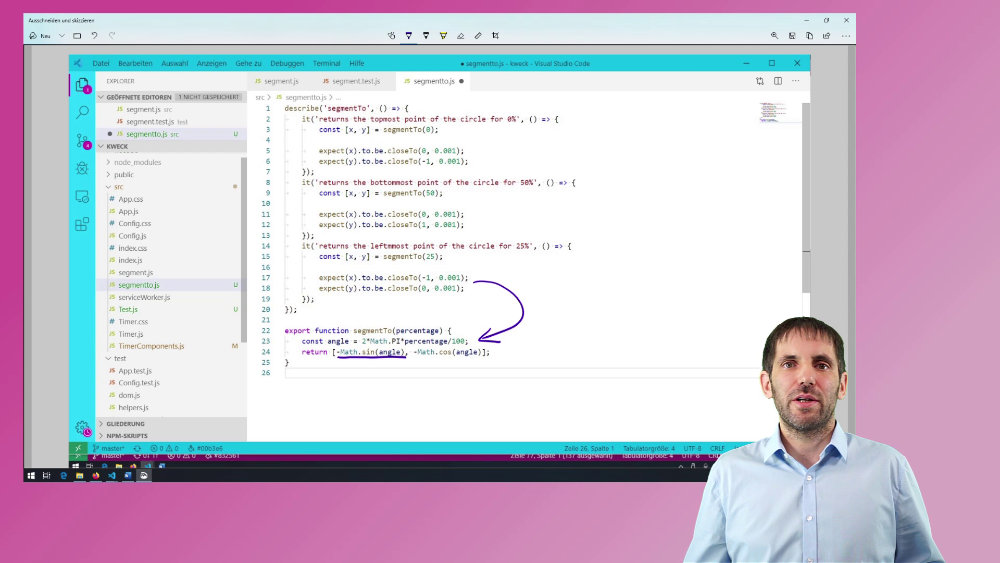
This last test also reinforces my choice of minus cosinus for the y coordinate, because the function is zero at this point.
Conclusion
I already almost knew how the final implementation of how my function would look like. But by writing only three very simple tests, I was able to break down the implementation into three even smaller steps and to be sure I did nothing wrong in any of the three steps.
And I can now automatically show that this function works because it produces the correct results for three important points.
And that’s all I need here. I did not need more examples to drive the implementation, and I do not need more examples to show that it works (given the future reader knows trigonometry).
Later I added a radius parameter to the function, so I added three more tests.
CTA
Do you test-drive your code when you already know the algorithm? How do you do that? Please tell me in the comments of this video - Let’s have a discussion! Or do you have any questions? Please also add a comment and I will try to answer your question.
Also, follow me on Twitter, I am @dtanzer there. There I will announce my next video about switching from TDD mode to doing a Spike. Also check out our training offers at devteams.at/services/trainings.
Read / watch all parts of “React TDD” here:

